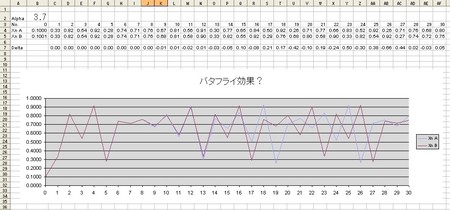
しばらく前にid:pal-9999さんに大変興味深いエントリーを教えていただいた。ぼんやりおもしろいなぁで最初終わってたんだけど、やっと思い出した。
僕:「その場合にだよ、CDOの繁殖は一体、何処で止まるのかな?」
(中略)
家内:「移入種が島で繁殖して、栄えた場合、それを止める要因はただひとつ。それはそれらの生命体を経済的に支えることが出来るだけの環境的リソースのキャパシティーが限界に達したときよ。つまり上の数式で N/K の K が小さいと (1−N/K) がマイナスになっちゃうわけ。そうなるとこの移入種は加速度的に自滅するわ。」
問題はNでもKでもない。rなのではないだろうか?
この式の形はそのまま「ロジスティック式」だ。
wikipediaのロジスティック式の項目の最後にこうある。
なお、この式をさらに追求すれば、非周期的にあらゆる値をとる場合にまでいたるさまざまな形が出現し、これに対してカオスという言葉を当てたのがカオス理論の始まりの一つである。
ロジスティック式 - Wikipedia
バタフライ効果 - HPO:機密日誌
rが一定の値を超えると、各世代間の個体数に規則性がなくなり、カオスになるのだ。つーか、この式の研究からカオスが生まれた。
3.56995
カオス理論 - Wikipedia
ということは、CODのような繁殖性の高い金融商品が主力の種となる金融商品個体生態系(=市場)が存在するならば、その生態系のふるまいは事実上予測不可能であるということになる。
そう考えると、ここのところの株価のあまりの上下はすでに金融市場はカオスであるということの証明であるかのように思える。
それは、金融市場が「共同現象」であり、「創発」ではないと見切った安冨先生の予言どおりということになる。

生きるための経済学―“選択の自由”からの脱却 (NHKブックス)
- 作者: 安冨歩
- 出版社/メーカー: 日本放送出版協会
- 発売日: 2008/03
- メディア: 単行本
- 購入: 11人 クリック: 245回
- この商品を含むブログ (70件) を見る
■余談
片一方で、ロジスティック式の解のひとつがシグモイドであり、そのまた先にはべき分布がある。このことは安冨先生の市場の選択はありえないとする見解へのアンチテーゼにつながりそうな気がしているが、まだ言葉が十分に私の中で熟していない。
この辺の生成と死滅とべき乗の法則との関連性についての原理原則というものを切に知りたいと感じる。その答えは、理論的な複雑系、複雑ネットワークの研究というよりも、多分生態学、生物学の系統からもたらされるような気がしてならない。
シグモイド、べき分布、そして複雑ネットワークとしての生態学 the beauty of sigmoid: HPO:個人的な意見 ココログ版
いや、そう言ってしまうのは早計かもしれない。考えてみれば、3年も前から疑問に思っているのだが、公文先生と安冨歩先生の間でご交流がないわけはない。
本書はこうした情報社会の変遷への興味を出発点として、シグモイド曲線に似た「S字波」をモチーフとした文明論、地域通貨への洞察、そして、べき乗則の世界へと展開されていく。実に私と関心が共通なことにびっくりした。参考図書のリストに、バラバシや、高安先生があがっていたのもうれしい。安冨先生の論文はご存知なのだろうか?鈴木健さんがGLOCOMにいらっしゃるから、きっともうご存知なんだろうな。
[書評]情報社会学序説 At home in the last modern: HPO:個人的な意見 ココログ版
大変失礼な言説かもしれないが、ロジスティック式とか、その微分解といった方向でなく文明批評ともいえる立場からシグモイドにたどりつかれた公文先生ってすばらしい。
ちなみに、シグモイド的S字がクルーグマンの「自己組織化の経済学」につながっている。
クルーグマンは、いとも簡単に自己組織化を目に見えるようにしてしまう。例えば、技術の優位性による普及率の均衡の変化を示すこのグラフだ。
[書評]自己組織化の経済学 その1 ~ 断続平衡 ~ S Curve: HPO:個人的な意見 ココログ版