大変、面白かった。

- 作者: 山口昌哉
- 出版社/メーカー: 筑摩書房
- 発売日: 2010/12/10
- メディア: 文庫
- 購入: 1人 クリック: 13回
- この商品を含むブログ (9件) を見る
finalventさんが、cakesに書かれていたのを読んで、ずいぶん前に買ってあった本書を読み始めた。
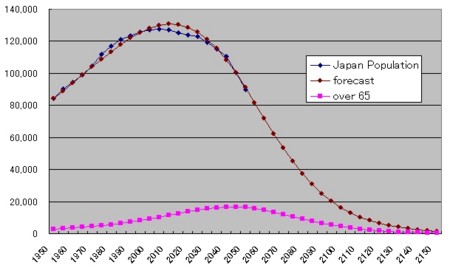
本書の冒頭で説明されるロジスティクス式については、その発展形であるロトカ=ヴォルテラ式を日本と世界の人口予想でいじったことがある。結構フィットした。
捕食人口の恐ろしさ、あるいは世界のすみっこで日本の滅亡を叫ぶ - HPO:機密日誌
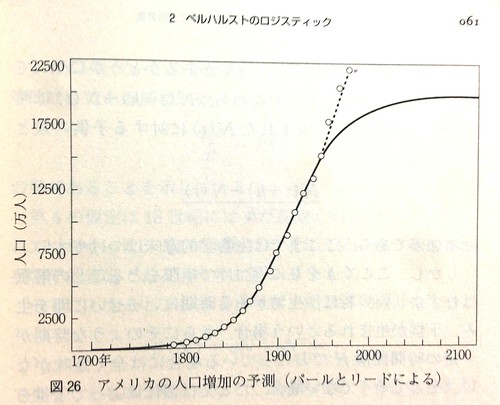
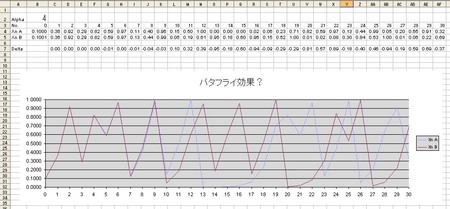
このロジスティクス式のグラフは、本書の67ページのこのグラフと原理的に同じ式で生成されている。
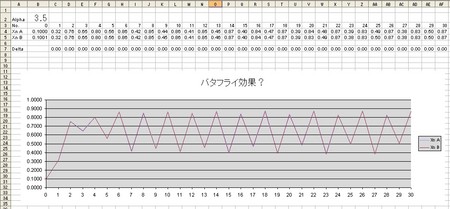
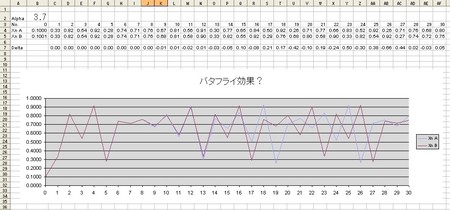
ロジスティクス式から係数を変えて、カオスの生成もやってみた。
私はどうしても心理学バックグランド、統計学バックグランドなので、決定論的なカオスの軌道のふるまいよりも、カオスの軌道を分布としてとらえて、近似モデルなのだとしてとらえてしまう。量子の分布も、たぶん捉え方によってはカオスの軌道の濃淡だとして表現しうると私には思えるのだが、軌道/分布でいえば、解説にもあったように「非線形、不安定性、自立系」ということになるのだろう。
本書の中にも乱数の生成のアルゴリズムが紹介されている。統計学では、対象の分布を想定する。これはつまり、なんらかのメカニズムが観察対象にあるはずなので、それに合わせた合理的なサンプルの分布があるはずだという仮定だ。本書の第一章で生成される乱数は、ラジオのノイズのような一様な分布になるはず。一般に一番統計で使われているのはガウシアンと呼ばれる、正規分布だ。他にも二項分布などごくごく数学的に仮定、生成される分布もある。タレブの「ブラックスワン」で強調されるのは言うまでもなくべき分布だ。これらの分布をする乱数も、非線形な式の形で表現されるし、生成されうる。
もう少し議論しなければならないポイントがいくつかあるのだが、あまりに眠いので今日はこの辺にしておく。今更ながらだが、勉強がたりないな、私。