非常によい方向性だと私は想う。
同ウイルスは感染者の約8割が無症状か軽症とされ、抗体保有率を調べることで感染者全体の推計や流行状況の把握につなげる。
同省などによると、検査は数千人を無作為に抽出して実施する見通し。今年度補正予算案に関連経費約2億円を盛り込んでいる。月内にも抗体検査実施 数千人対象、保有率調査 新型コロナの感染実態把握・厚労省(時事通信) - Yahoo!ニュース
https://news.yahoo.co.jp/pickup/6357901
ニューヨークのクオモ知事はロックダウンの解除の判断材料として抗体検査を使うと明言されていると聞く。
抗体検査についてはツイッターで議論させていただいた。感染経験者が母集団である日本国民、もしくは東京都民の中でどれくらいの確率で存在していて、そのためにランダムサンプリングの対象数は何ケースくらい必要かということにようやく意識できた。
あらⓅ★ @arapix9日前
100人のうち10人が検査して1人が感染してたから、全体の10人(あと9人)が感染してるはず、と考えるのは間違ってる。潜在的な感染者は居るだろうが、平準化するのは違う。ひでき @hidekih9日前
arapix 統計の授業をまじめに聞いてなかったので生なかですが、大体の出現率がわかっていればサンプリングが可能です。例えば、全人口の10%が感染しているとわかっていれば(私の理解では)100人のうち10人ランダムサンプリングすればいいですし、1%の確率だと100のサンプリングとなります。すみません、私の説明では伝わらないですよね。
意外と知らない?!サンプル数の正しい考え方ひでき @hidekih9日前
yuki073 統計学の基本なのですが、ランダムサンプリングが保証されていれば5%誤差で600程度、1%誤差で1200程度のケースが取れれば、母集団(日本の国民)の推計ができます。現在のPCR検査は発症等した特殊ケースでランダムサンプリングになっていないので、何件とっても母集団の推計統計ができません。ゆーき @yuki0739日前
hidekih ですから、想定される日本国民全体から見た感染率が1%を余裕で下回る状態で、1%誤差の統計を取って意味があると?そもそも日本国民全体の感染率だと偽陽性率のほうが高いのでは?ひでき @hidekih8日前
yuki073 なるほど。社会調査で使われる早見表などでは母集団の1%の陽性があったとして、精度を0.4%をするには3,000標本となります。偽陽性の確率がランダムサンプリングと同様、一貫して30%程度であれば、たぶん1万くらいのランダムサンプリングとなるのではないでしょうか?ゆーき @yuki0738日前
hidekih 日本全体の感染率が低すぎて偽陽性率の調査にしかならないと言ってるのが理解できないのか?偽陽性の意味と統計に与える影響は理解されいていますか?ひでき @hidekih8日前
yuki073 すみません、失礼しました。感染率については行動変容の観点から計算しなおしてみました。全人口に対して潜在している感染者をどう見積もっても0.02%くらいです。0.1%いかないですね。1万ケースのランダムサンプリングでは誤差の範囲内に入ってしまいます。ひでき @hidekih8日前
Covid19による重篤者、死亡者数をどう受け止めるかについての議論 - Togetter
数字で納得すべきでした。
docs.google.com
最後の表でまとめたように、この時点で顕在化している感染者数が七千人あまりだったので、仮に実際の感染者はその倍存在していても、日本国民全体からすれば0.02%程度の存在確率となってしまう。これでは抗体検査の精度の悪さの問題もあり、数十万人のランダムサンプリングが必要ということになり抗体検査は意味がないと一旦は考えた。
しかし、カリフォルニアの抗体検査では日本でも多く伝えられているように、顕在している感染者の50倍から80倍の感染経験者がいることを明らかにしたと伝えられた。
で、あれば日本政府は抗体検査を行って、現実の感染状況を把握した上で、今後の政策決定を行うべきだと私は主張した。
厚労省の発表で若干不明確なのは、カリフォルニアも、ニューヨークも「州」という一千万人程度の母集団での検査であるのに、母集団の定義がされていないことだ。上記の議論からわかるように、抗体検査の「誤差」が三割程度あるのだとすれば、日本全国で調査を行うのなら、
11,350人(2/22時点、厚労省発表) x 50倍(加州結果から推測)/約126,500,00=0.45% < 1%
仮に3,000ケースの標本だとして誤差を計算すると、
誤差確率=2 x sqrt(0.45%x(1-0.45%)/3,000)) = 0.24%
統計学に明るくない私はこういうことをしてよいのかは確信がないが、
0.24% / 0.45% = 約5割
となるので、抗体検査の誤差に「負けて(誤差の混入?)」しまうのではないだろうか?同様の計算で調査対象が1万ケースだと、
0.13% / 0.45% = 約3割
でぎりぎりかなと。
東京都では、
都民人口=9,273,000人
顕在感染者=3,320人
想定感染確率=3,3,20 x 50倍 / 9,273,000 = 1.7%
誤差確率=2 x sqrt(1.7%x(1-1.7%)/3,000)) = 0.47%
0.47% / 1.7% = 約3割
となり、「数千人」の標本数のランダムサンプリングでも統計上有意な結果が得られるそう。であれば、東京都に絞るのもひとつの案となると考える。もちろん、厚労省、専門家の方々は十分に調査計画を検証してから行われるのだと思うので、私のような素人がどうのいうことではないが、どうせやるなら、統計的妥当性を担保していただきたいものだと。
大事なのは、もしこれでカリフォルニア、あるいはドイツの同様の研究のように、人口のかなりの割合で既に感染済であれば、緊急事態宣言後に段階的自粛緩和を行い、高齢者を「囲い込み」する方向の政策となる。調査でほとんど見つからず、実際の感染者をかなりの割合で把握できているのであれば、「グリーン化」(ウィルスの囲い込み)を目指して、更に自粛を続けるべきだということになる。
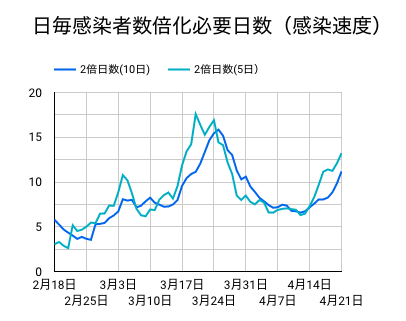
緊急事態宣言による外出自粛は当初発表された通りではないにせよ、確実に効果をあげている。
https://datastudio.google.com/s/vFUiTvp_70M
ちなみに、抗体検査の検定にあたっては、献血の血が用いられるらしい。結果は知らされないということだが、献血に行きたくなる。
https://news.tbs.co.jp/newseye/tbs_newseye3962631.htmlnews.tbs.co.jp
まさに正念場だなと。安倍総理大臣を心から応援したい気持ちでいっぱい。
■追記
カリフォルニアの検査には、Facebookで検査対象者を募ったこと、抗体検査の正確さなど問題ありとの指摘が。
新型コロナ抗体検査結果
— 徳田安春(Yasuharu Tokuda, MD MPH)医師、筑波大客員教授、群星沖縄センター長 (@yasuharutokuda) 2020年4月23日
スタンフォード大学の研究結果に致命的なバイアスあり
やはりPeer Review は大切https://t.co/r86N9R52fX
やはり、統計的厳密さ、ランダムサンプリングの徹底は絶対かなと。
■追記 その2 2020/5/15
1ヶ月、いや2ヶ月遅れで実施との報道。5月1日発表という話しはどうなってしまったのか?